gráfica de las transformaciones de la energía

Si bien la energía cinética (${\displaystyle E_{c}}$) de un cuerpo es una propiedad física que depende de su movimiento, la energía potencial (${\displaystyle E_{p}}$), en cambio, es un concepto de energía que va a depender del tipo de interacción que se ejerce sobre el cuerpo, de su posición y de la configuración en el espacio del citado cuerpo o cuerpos sobre los que se aplica. Así en una situación ideal en la que los objetos que constituyen el sistema físico en estudio estén ausentes de fricción, entonces la suma de ambas energías, cinética y potencial, va a representar la energía total del sistema, ${\displaystyle E}$, y se va a conservar, independientemente de la posición o posiciones que vaya ocupando el sistema en el tiempo.⁴​

La noción de energía potencial se relaciona con el trabajo realizado por las fuerzas sobre el sistema físico para trasladarlo de una posición a otra del espacio. La función energía potencial dependerá de forma importante del tipo de campo de fuerzas o interacción que actúe sobre el sistema. Por ejemplo, la fuerza de gravitación, la electromagnética, responsable de las interacciones eléctrica y magnética, o la elástica (derivada de la electromagnética). Si el trabajo no depende del camino seguido, entonces a la fuerza ${\displaystyle {\overrightarrow {F}}}$ se le llama conservativa y el trabajo ${\displaystyle W}$ expresa la diferencia de energía potencial ${\displaystyle E_{p_{A}}-E_{p_{B}}}$ del sistema entre la posición de partida (A) y la posición de llegada (B).⁵​

${\displaystyle W_{AB}=\int _{B}^{A}{\overrightarrow {F}}\cdot \,{\overrightarrow {dl}}=E_{p_{A}}-E_{p_{B}}\qquad \qquad }$

También se utiliza la función potencial ${\displaystyle V}$ en lugar de la energía potencial ${\displaystyle E_{p}}$ para representar el trabajo realizado por la unidad básica de la interacción. Si, por ejemplo, la interacción es la gravitatoria, sería la unidad de masa y en el caso de la interacción eléctrica, la unidad de carga.

La función energía potencial y, en especial, la función potencial, tienen gran interés en la física no solo cuando se aplican a las interacciones que son importantes a nuestra escala, como son la gravitatoria, la electromagnética y la elástica (derivada de la electromagnética), sino también cuando se estudia cualquier tipo de fuerza o interacción, incluso en la física cuántica al tratar de resolver la dinámica de un sistema físico mediante la ecuación de Schrödinger.⁶​ Se aplica, por ejemplo, a la física atómica en la obtención de los estados electrónicos del átomo o en la física molecular, para la obtención de los estados electrónicos, de vibración, de vibración-rotación y de rotación de la molécula, así como en la física del estado sólido. También se aplica en la física nuclear.⁷​

En otras formulaciones más generales de la física, la función potencial juega, así mismo, un papel importante. Entre ellas, las formulaciones lagrangiana y hamiltoniana de la mecánica.⁸​

La energía potencial gravitatoria se define como la energía que poseen los cuerpos por el hecho de poseer masa y estar situados a una determinada distancia mutua. Entre las masas de grandes magnitudes se ejercen fuerzas de atracción, de mayor intensidad cuanto mayores son estas. Aplicado, por ejemplo, al movimiento planetario, la masa mayor es la del sol que crea un campo de fuerzas gravitatorio que actúa sobre las masas menores de los planetas. A su vez, cada planeta crea un campo de fuerzas gravitatorio que actúa sobre las masas menores que estén próximas al planeta, los satélites.⁹​

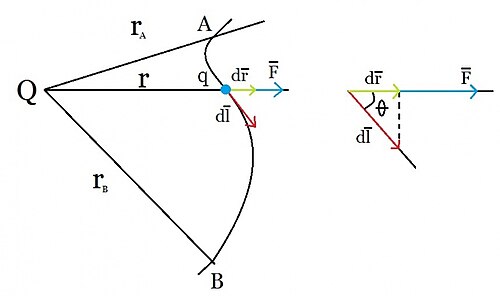
El trabajo realizado para llevar una masa de prueba m en presencia de otra masa M, fuente del campo gravitatorio, desde un punto A a otro B, es la diferencia de la energía potencial de la masa m en el punto de partida A menos la energía potencial en el punto de llegada B. El citado trabajo no depende del camino seguido sino tan solo de los puntos inicial y final. Al gozar de esta propiedad la fuerza gravitatoria y el campo gravitatorio (la fuerza gravitatoria sobre la unidad de masa), al campo se le llama campo conservativo y tiene pleno sentido obtener el potencial gravitatorio, derivado del campo creado por la masa M, así como la energía potencial gravitatoria derivada de la fuerza gravitatoria entre las masas m y M.

Si se considera una masa M en el origen del sistema de coordenadascomo fuente del campo gravitatorio y se elige como referencia el infinito, punto en el que cualquier masa m tiene una energía potencial nula, la energía potencial es el trabajo necesario para llevar la masa m desde el infinito hasta un determinado punto A definido por la coordenada ${\displaystyle r}$ (la distancia del punto A al origen de coordenadas).⁹​

${\displaystyle W=E_{p_{A}}-E_{p_{\infty }}=}$ ${\displaystyle \Delta E_{p}=-\int _{\infty }^{A}F_{g}\cdot \,dr=-\int _{\infty }^{A}{\frac {G\cdot M\cdot m}{r^{2}}}\cdot \,dr=G\cdot M\cdot m\cdot \left\lbrack {\frac {1}{r}}\right\rbrack _{\infty }^{A}={\frac {G\cdot M\cdot m}{r_{A}}}=E_{p_{A}}\qquad \qquad [1]}$

Donde: ${\displaystyle E_{p}}$ es la energía potencial gravitatoria de la masa ${\displaystyle m}$, cuyo valor depende de la distancia ${\displaystyle r}$ entre la masa de prueba ${\displaystyle m}$ y la masa ${\displaystyle M}$ que genera el campo gravitatorio, y se mide en julios (${\displaystyle J}$). Por otro lado, ${\displaystyle F_{g}={\frac {G\cdot M\cdot m}{r^{2}}}}$ es la fuerza gravitatoria sobre la masa de prueba ${\displaystyle m}$ situada a una distancia ${\displaystyle r}$ de la masa ${\displaystyle M}$ que crea el campo gravitatorio y se mide en newtons (${\displaystyle N}$). Además, ${\displaystyle G}$ es la constante de gravitación universal, cuyo valor es ${\displaystyle G=6.673\times 10^{-11}\;\left({\cfrac {{\text{N}}\cdot {\text{m}}^{2}}{{\text{kg}}^{2}}}\right)}$. Finalmente, ${\displaystyle M}$ y ${\displaystyle m}$ se miden en kilogramos (${\displaystyle kg}$) ${\displaystyle R}$ es la distancia que separa las dos masas, medida en metros (${\displaystyle m}$)

La ecuación [1] que representa la energía potencial ${\displaystyle E_{p_{A}}}$ de las masas m y M cuando están separadas una distancia ${\displaystyle r_{A}}$, es aplicable tanto a masas puntuales como a masas con simetría esférica, siendo la distancia entre ellas, la que hay entre los centros de dichas esferas.

La energía potencial cerca de la superficie de la Tierra[editar]

La energía potencial que posee una masa ${\displaystyle m}$ situada a una altura ${\displaystyle h}$ sobre la superficie terrestre vale:

${\displaystyle \Delta E_{p}=m\cdot g\cdot h\qquad \qquad [2]}$

Esta expresión es un caso particular de la ecuación anterior [1]. Dicho caso se presenta cuando la masa se encuentra a una altura pequeña sobre la superficie de la tierra. Para demostrarlo, basta con aplicar la expresión [1] y considerar la variación de energía potencial entre las alturas sobre la superficie de la tierra, ${\displaystyle h_{1}}$ y ${\displaystyle h_{2},(h_{1}\ll R_{t},h_{2}\ll R_{t}}$ y ${\displaystyle h_{2}>h_{1})}$ siendo ${\displaystyle R_{t}}$el radio de la tierra.¹⁰​

${\displaystyle \Delta E_{p}=E_{p2}-E_{p1}=G\cdot M\cdot m\cdot \left({\frac {1}{R_{t}+h_{1}}}-{\frac {1}{R_{t}+h_{2}}}\right)=}$ ${\displaystyle =E_{p2}-E_{p1}=G\cdot M\cdot m\cdot {\frac {(h_{2}-h_{1})}{R_{t}^{2}+R_{t}\cdot (h_{2}+h_{1})+h_{1}\cdot h_{2}}}\approx G\cdot M\cdot m\cdot {\frac {h_{2}-h_{1}}{R_{t}^{2}}}\qquad \qquad [3]}$

En este caso, los productos ${\displaystyle R_{t}\cdot h_{2},R_{t}\cdot h_{1}}$ y ${\displaystyle h_{1}\cdot h_{2}}$ son muy pequeños comparados con ${\displaystyle R_{t}^{2}}$ y, por lo tanto, se pueden despreciar en la ecuación [3].

Llamando ${\displaystyle g=G\cdot M\cdot {\frac {1}{R_{t}^{2}}}}$

${\displaystyle E_{p2}-E_{p1}=m\cdot g\cdot (h_{2}-h_{1})}$

Si se toma ${\displaystyle h_{1}}$ como el origen de energías potenciales, por ejemplo, al nivel del mar y llamando ${\displaystyle h_{2}=h}$:

${\displaystyle \Delta E_{p}=m\cdot g\cdot h}$

Del desarrollo anterior se deduce que para ${\displaystyle h\ll R_{t}}$ la aproximación última es adecuada.

Velocidad de escape[editar]

La velocidad de escape es la velocidad mínima necesaria para que un cuerpo de masa ${\displaystyle m}$ salga fuera de la atracción gravitatoria.¹¹​

La fuerza de gravitación es conservativa. La energía potencial ${\displaystyle E_{p}(r)}$ de una masa ${\displaystyle m}$ es:

${\displaystyle E_{p}(r)=-G\cdot {\frac {m\cdot M}{r}}}$

Para que el cuerpo escape a la acción del campo gravitatorio la energía total ${\displaystyle E_{t}}$ del mismo debe ser positiva o nula, es decir, debe suceder que la energía cinética supere o, al menos iguale, la energía potencial. En el caso umbral estaremos calculando la velocidad de escape.¹²​ Se puede calcular en el caso de la Tierra.

${\displaystyle E_{T}=0}$

${\displaystyle E_{t}=E_{c}+E_{p}=0\Rightarrow {\frac {1}{2}}\cdot m\cdot v_{e}^{2}=G\cdot {\frac {m\cdot M}{r}}}$

${\displaystyle v_{e}={\sqrt {\frac {2\cdot G\cdot M}{r}}}={\sqrt {2gr}}}$ ${\displaystyle (m/s)}$

donde ${\displaystyle r}$ es la distancia radial o posición del cuerpo de masa ${\displaystyle m}$ con respecto a la masa ${\displaystyle M}$ que genera el campo gravitatorio¹³​

Velocidad de escape de la superficie de la Tierra

${\displaystyle G=6.674\cdot 10^{-11}\;{\cfrac {{\text{N}}\cdot {\text{m}}^{2}}{{\text{kg}}^{2}}}}$

${\displaystyle M_{T}=5,97\cdot 10^{24}}$ ${\displaystyle kg}$

${\displaystyle R=6,37\cdot 10^{6}}$ ${\displaystyle m}$

Sustituyendo los datos se obtiene:¹⁴​

${\displaystyle v_{e}={\sqrt {\frac {2\cdot G\cdot M_{T}}{R}}}={\sqrt {\frac {2\cdot 6,67\cdot 10^{-11}\cdot 5,97\cdot 10^{24}}{6,37\cdot 10^{6}}}}\approx 11,17\cdot 10^{3}}$${\displaystyle m\cdot s^{-1}}$

Si el móvil supera la velocidad de escape abandonaría todavía con más facilidad la acción del campo gravitatorio terrestre.

Superficies equipotenciales[editar]

El potencial gravitatorio se define como la energía potencial por unidad de masa:

${\displaystyle V={\frac {E_{p}}{m}}}$

Y por tanto se obtiene:

${\displaystyle V(r)={\frac {G\cdot M}{r}}}$

Donde ${\displaystyle V}$ es la energía potencial de la unidad de masa, o potencial, a una distancia ${\displaystyle r}$ de la masa ${\displaystyle M}$. Las unidades de ${\displaystyle V}$ en el S.I. son ${\displaystyle {\frac {J}{kg}}}$.

G es la constante de gravitación universal.

M es la masa del objeto que crea el campo y, por tanto, estará medida en ${\displaystyle kg}$.

Si M es puntual o de geometría esférica, las superficies equipotenciales (superficies de potencial constante) son la familia de esferas definidas por la familia de superficies:

${\displaystyle V_{i}={\frac {G\cdot M}{r_{i}}}=C_{i}\ ,\qquad i=1,2,3...}$

siendo ${\displaystyle C_{i}}$ constantes arbitrarias cuyo valor numérico representa el potencial gravitatorio asociado a cada valor de la posición ${\displaystyle r_{i}}$.

Las superficies equipotenciales gravitatorias terrestres son todas las esferas con centro en el de la Tierra.

El dibujo de una montaña rusa en un plano se puede interpretar como la representación de la función energía potencial ${\displaystyle E_{p}}$ de un cuerpo en el campo gravitatorio. Cuanto más sube un móvil la montaña rusa, mayor es su energía potencial y menor su energía cinética ${\displaystyle E_{c}}$, y por tanto se desplaza más lento. En los máximos relativos de dicha función (los picos de la montaña rusa) su energía potencial será más elevada que en los puntos de su entorno. Estos puntos se llamarán puntos de equilibrio mecánico inestable, ya que si se deposita en ellos un objeto con ${\displaystyle v=0}$por poco que se desplace de ese punto, el objeto siempre tenderá a alejarse. Por otro lado, si lo situamos en los mínimos de la función (los valles de la montaña rusa), el móvil que los abandonase en uno u otro sentido siempre tenderá a volver hacia ellos, son los puntos llamados puntos de equilibrio estable.¹⁵​ Como la energía mecánica ${\displaystyle E}$ del cuerpo se conserva ${\displaystyle E=E_{c}+E_{p}=E_{cmax}=E_{pmax}}$ , en la figura.

Péndulo[editar]

En el caso de un péndulo, cuyo movimiento puede alcanzar una altura ${\displaystyle h}$ medida a partir de su posición más baja, también se puede comprobar la ley de conservación de la energía. En los puntos más altos (altura h), donde la energía potencial es máxima, la velocidad del péndulo es nula y el movimiento cambia de sentido. Por otro lado, la posición más baja, que se pude llamar ${\displaystyle P}$, será aquella con una mayor energía cinética y velocidad máxima pero con una energía potencial mínima. La posición ${\displaystyle P}$ se podrá tomar como origen de la energía potencial (se le puede asociar una energía potencial nula).

Si se coloca una masa m sujeta a un extremo del muelle y se separa una distancia x de su posición de equilibrio, x=0, este comenzará a oscilar con un movimiento armónico simple. En este movimiento el bloque posee una energía cinética y una energía potencial. Al ser la fuerza elástica que satisface la ley de Hooke una fuerza conservativa, se puede derivar la función energía potencial, bajo la acción de la fuerza elástica del muelle. Así, el trabajo realizado para estirar el muelle una distancia x desde su posición de equilibrio, oponiéndose a la fuerza del muelle es:²³​

${\displaystyle W=E_{p}(x)=\int _{0}^{x}-F_{x}dx=\int _{0}^{x}-(-kx)dx={\frac {1}{2}}kx^{2}\qquad \qquad }$

Este trabajo representa la energía potencial Ep que tiene el bloque en la posición x. Para ello se ha convenido en asociar la E_p = 0 a la posición x=0 (origen de la función potencial). Si ahora se calcula el trabajo para desplazar el bloque de una posición ${\displaystyle x_{1}}$ a otra ${\displaystyle x_{2}}$, se comprueba que este solo depende de las posiciones inicial y final:²³​

${\displaystyle W=E_{p}(x_{2})-E_{p}(x_{1})=\int _{x_{1}}^{x_{2}}-kxdx={\frac {1}{2}}k(x_{1}^{2}-x_{2}^{2})}$

En la figura se puede observar la función energía potencial Ep (x) como una parábola centrada en x=0, función de la posición x. La recta de pendiente -k, es la fuerza elástica correspondiente ${\displaystyle {\vec {F_{el}}}=-kx{\vec {u_{x}}}}$. A la vez se representa la cantidad estirada del muelle en función de su posición x. Si con una fuerza F se produce un desplazamiento x, con la fuerza 2F el desplazamiento es también el doble, 2x. La parte negativa del eje x representa el desplazamiento de la masa cuando el muelle está comprimido.

Curva de energía potencial elástica y fuerza correspondiente aplicado a la respuesta de una bola sujeta a un muelle

Propiedades de la curva de energía potencial[editar]

• Pendiente de la curva ${\displaystyle E_{p}(x)}$ :

${\displaystyle Fuerza:{\vec {F}}=-{\frac {dE_{p}}{dx}}\ {\vec {u_{x}}}=-kx{\vec {u_{x}}}}$

Si ${\displaystyle x>0}$

${\displaystyle {\frac {dE_{p}}{dx}}=kx>0\quad 'pendiente\quad positiva'}$

Si ${\displaystyle x<0}$

${\displaystyle {\frac {dE_{p}}{dx}}=kx<0\quad 'pendiente\quad negativa'}$

• Punto de equilibrio:

${\displaystyle {\frac {dE_{p}}{dx}}=kx=0\Rightarrow x=0}$

${\displaystyle {\frac {d^{2}E_{p}}{dx^{2}}}=k>0}$ es un mínimo

Energía potencial electrostática y potencial eléctrico[editar]

Artículo principal: Energía potencial electrostática

La variación de la energía potencial representa un trabajo realizado por una fuerza conservativa. Del mismo modo que la fuerza de atracción entre dos masas es conservativa, también la fuerza eléctrica o fuerza de Coulomb ${\displaystyle F_{el}}$ entre dos cargas es conservativa, siendo de repulsión si tienen el mismo signo y de atracción si son de signo opuesto. Los objetos que se repelen tienen mayor energía potencial cuanto menor es la distancia entre ellos, y si se atraen es mayor su energía potencial cuanto mayor es la distancia entre ellos, como veremos a continuación.

El trabajo de una fuerza conservativa es igual a la diferencia entre el valor inicial y el valor final de una función, la energía potencial, dado que solamente dependerá de las posiciones inicial y final y no de la trayectoria seguida. Las fuerzas electrostáticas originadas por cargas eléctricas son conservativas y el trabajo realizado por estas fuerzas no dependerá de la trayectoria seguida:

${\displaystyle W=\int _{A}^{B}{\vec {F}}_{el}\cdot d{\vec {l}}=E_{pA}-E_{pB}\,\!}$

siendo ${\displaystyle E_{p}}$ la función energía potencial y ${\displaystyle E_{pA}}$ y ${\displaystyle E_{pB}}$ los valores de la energía potencial en las posiciones A y B.²⁴​

Si se coloca una masa m sujeta a un extremo del muelle y se separa una distancia x de su posición de equilibrio, x=0, este comenzará a oscilar con un movimiento armónico simple. En este movimiento el bloque posee una energía cinética y una energía potencial. Al ser la fuerza elástica que satisface la ley de Hooke una fuerza conservativa, se puede derivar la función energía potencial, bajo la acción de la fuerza elástica del muelle. Así, el trabajo realizado para estirar el muelle una distancia x desde su posición de equilibrio, oponiéndose a la fuerza del muelle es:²³​

${\displaystyle W=E_{p}(x)=\int _{0}^{x}-F_{x}dx=\int _{0}^{x}-(-kx)dx={\frac {1}{2}}kx^{2}\qquad \qquad }$

Este trabajo representa la energía potencial Ep que tiene el bloque en la posición x. Para ello se ha convenido en asociar la E_p = 0 a la posición x=0 (origen de la función potencial). Si ahora se calcula el trabajo para desplazar el bloque de una posición ${\displaystyle x_{1}}$ a otra ${\displaystyle x_{2}}$, se comprueba que este solo depende de las posiciones inicial y final:²³​

${\displaystyle W=E_{p}(x_{2})-E_{p}(x_{1})=\int _{x_{1}}^{x_{2}}-kxdx={\frac {1}{2}}k(x_{1}^{2}-x_{2}^{2})}$

En la figura se puede observar la función energía potencial Ep (x) como una parábola centrada en x=0, función de la posición x. La recta de pendiente -k, es la fuerza elástica correspondiente ${\displaystyle {\vec {F_{el}}}=-kx{\vec {u_{x}}}}$. A la vez se representa la cantidad estirada del muelle en función de su posición x. Si con una fuerza F se produce un desplazamiento x, con la fuerza 2F el desplazamiento es también el doble, 2x. La parte negativa del eje x representa el desplazamiento de la masa cuando el muelle está comprimido.

Curva de energía potencial elástica y fuerza correspondiente aplicado a la respuesta de una bola sujeta a un muelle

Propiedades de la curva de energía potencial[editar]

• Pendiente de la curva ${\displaystyle E_{p}(x)}$ :

${\displaystyle Fuerza:{\vec {F}}=-{\frac {dE_{p}}{dx}}\ {\vec {u_{x}}}=-kx{\vec {u_{x}}}}$

Si ${\displaystyle x>0}$

${\displaystyle {\frac {dE_{p}}{dx}}=kx>0\quad 'pendiente\quad positiva'}$

Si ${\displaystyle x<0}$

${\displaystyle {\frac {dE_{p}}{dx}}=kx<0\quad 'pendiente\quad negativa'}$

• Punto de equilibrio:

${\displaystyle {\frac {dE_{p}}{dx}}=kx=0\Rightarrow x=0}$

${\displaystyle {\frac {d^{2}E_{p}}{dx^{2}}}=k>0}$ es un mínimo

Energía potencial electrostática y potencial eléctrico[editar]

Artículo principal: Energía potencial electrostática

La variación de la energía potencial representa un trabajo realizado por una fuerza conservativa. Del mismo modo que la fuerza de atracción entre dos masas es conservativa, también la fuerza eléctrica o fuerza de Coulomb ${\displaystyle F_{el}}$ entre dos cargas es conservativa, siendo de repulsión si tienen el mismo signo y de atracción si son de signo opuesto. Los objetos que se repelen tienen mayor energía potencial cuanto menor es la distancia entre ellos, y si se atraen es mayor su energía potencial cuanto mayor es la distancia entre ellos, como veremos a continuación.

El trabajo de una fuerza conservativa es igual a la diferencia entre el valor inicial y el valor final de una función, la energía potencial, dado que solamente dependerá de las posiciones inicial y final y no de la trayectoria seguida. Las fuerzas electrostáticas originadas por cargas eléctricas son conservativas y el trabajo realizado por estas fuerzas no dependerá de la trayectoria seguida:

${\displaystyle W=\int _{A}^{B}{\vec {F}}_{el}\cdot d{\vec {l}}=E_{pA}-E_{pB}\,\!}$

siendo ${\displaystyle E_{p}}$ la función energía potencial y ${\displaystyle E_{pA}}$ y ${\displaystyle E_{pB}}$ los valores de la energía potencial en las posiciones A y B.²⁴​